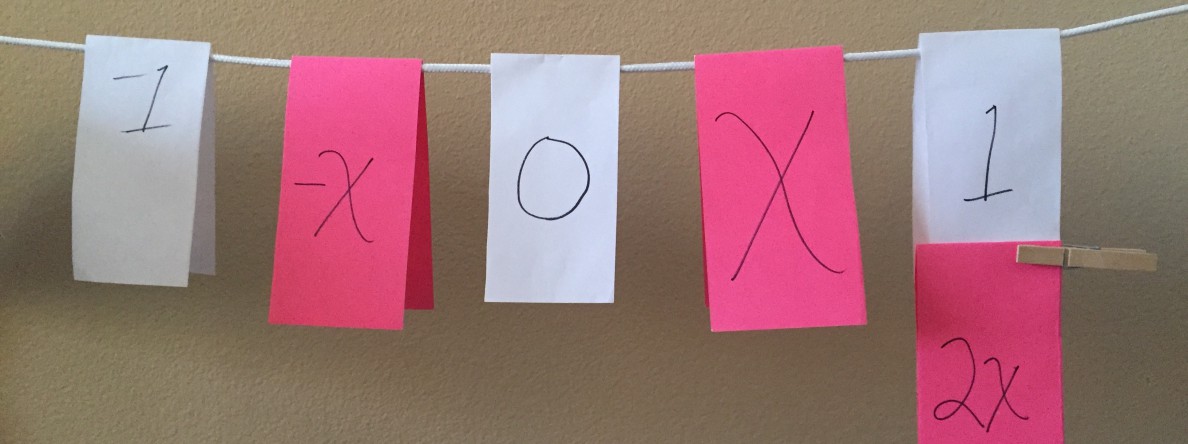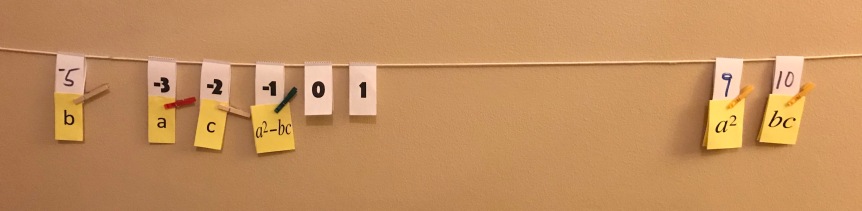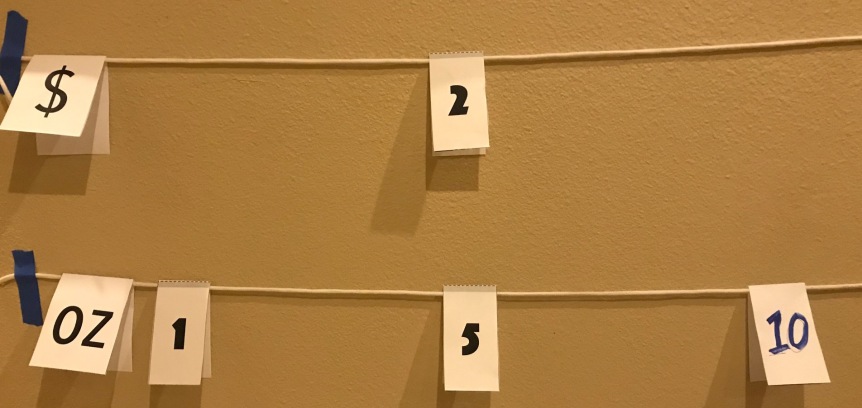My first experience with Clothesline Math was on a single line, so most of my early lessons were exclusive single number lines. I now make use of the single, double or triple clothesline depending on the nature of the math topic involved.
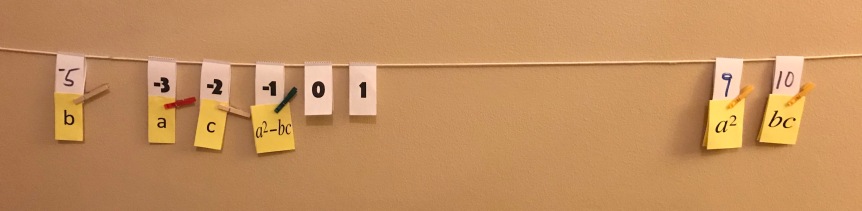


I must admit, though, I was slow to warm up to multiple clotheslines, mostly because I did not see the advantage of it. I thought, why put up a double clothesline when you can simply pin the values together?

However, when I saw the Yogurt Shop example by Kristen Bennett and Andrew Stadel, my eyes were opened to the instructional potential of multiple lines. The top line in the picture below represents the price of the yogurt serving; the bottom line represents the number of ounces in the serving. The example shows that a 5-ounce serving costs $2. It begs students to determine the cost of yogurt per ounce.
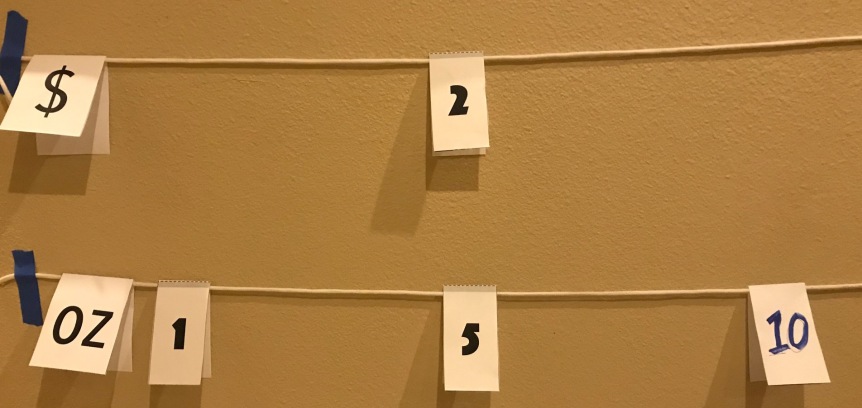
So how do I decide when a double or even triple clothesline is superior to a single? The criteria is simple: When the units being compared are the same or there is one function being analyzed, go single. When the units, the mathematical functions or the representations are different… go double or triple. In other words, multiple units, relationships or representations need multiple lines.
In our yogurt example above, it would not make sense to pin the ‘5’ to the ‘2,’ so a double line set-up is almost demanded. The units are different, so the two lines also help develop the concept of rate. Another terrific example of using a double clothesline to compare different units is in the conversion between degrees and radians.

Often times, it is not units that are different, but the representations as when comparing fraction, decimals and percentages. In this case it would be appropriate to pin say ‘0.5’ to ‘50%,” but it is more powerful, and less confusing, to have the three representations on three separate lines.

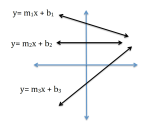
Multiple clotheslines are also effective when comparing different data sets in statistics or different functions in algebra.


For some topics, the multiple clotheslines are demanded for the sake of clarity and concept development. For many topics, it is a nice option, but the single may still work, as in the following example on operations with fractions.

As with all things in the classroom, your professional judgment will be needed to determine the best instructional move. Now that your eyes have seen what I see, you will now be capable to branch out and effectively customize your Clothesline lessons to the mathematical concept of the day.